Local symmetry
Local symmetry options are available in RELION v2.1 and above. The program has only limited support of RELION 3.1's new STAR format. For example, the program will give a wrong result for datasets with particles with different pixel sizes and/or box sizes. If you encounter a problem, please report to CCPEM.
For the standalone programs relion_localsym and relion_localsym_mpi, type the command relion_localsym --function_help for the full list of available functions and parameters, and relion_localsym [function] --function_help for the corresponding parameters of a specific function.
Definition of local symmetry in RELION
Local symmetry in RELION is implemented to average identical regions which cannot be simply related by overall symmetry (e.g. point group or helical) in cryo-EM density maps. Numbers of sets (N, N≥1) and identical regions (Ki, 1≤i≤N, Ki≥2) within each set can be arbitrary. The identical regions might be assembled into the whole structure, or they might only contribute to parts of densities which bind to other asymmetrical subunits.
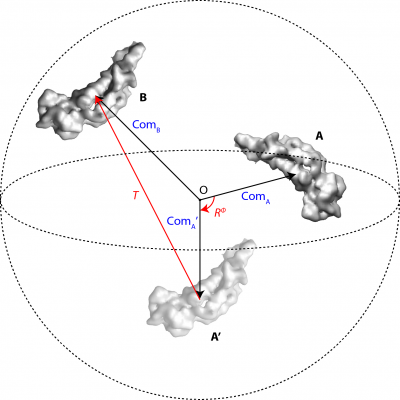
For each set of identical regions related by local symmetry, one soft-edged binary mask (Mi) is needed, covering any one of the asymmetrical subunits of the local symmetry. All the other regions are assumed to be identical in densities and their positions and orientations relative to the masked region are defined by local symmetry operators. Figure 1 shows a schematic example of a pseudo-dimer AB (N=1, K1=2) and the mask M1 covers the subunit A.
A transformation operator contains 6 parameters, 3 rotations φ, θ, ψ (following the definition of Euler angles in RELION) in degrees and 3 translations Δx, Δy, Δz in Angstroms. The pair of identical pieces of densities, A and B in Figure 1, corresponds to a unique operator Op = [φ, θ, ψ, Δx, Δy, Δz], which firstly rotates the masked region A to A’ around the centre O of the 3D particle box, and then translates the rotated densities A’ to fit onto the symmetry-related region B. The transformations are performed in real-space using trilinear interpolations. Note that all the symmetry-related regions must be located within the maximum sphere (dashed circle in Figure 1) inside the 3D particle box (D×D×D, in pixels) to avoid any loss of information during image transformations.
In order to impose local symmetry on a density map with N sets of identical regions, one mask is required for each set, which results in N masks in total. If the ith set contains of Ki (Ki≥2) identical regions, Ki–1 operators needs to be defined. For example, two masks (Mtri, Mtetra) are required for a complex that consists of a trimer of one protein that is bound to a tetramer of another protein. Mtri covers a monomer of the trimer (along with 2 operators) and Mtetra covers a monomer of the tetramer (along with 3 operators).
The mask should be in MRC format and of the same dimensions in pixels as the 3D density map. The position of a mask must correspond to the position of the subunit of the density map in its 3D data array. For example, assume that a density map with the size of 300×300×300 pixels contains the pseudo-dimer AB in figure 1. The x, y, z integer subscripts of the 3D map range from -150 to +149. The subunit A is written into positions with x, y, z subscripts of +50 ~ +100 (approx.) in the 3D data array. Therefore, the soft-edged binary mask of A must be of 300×300×300 pixels in dimensions, and the (0, 1] mask values must be written into x, y, z subscripts of +50 ~ +100 (approx.). It should be taken care of because a mask of another definition writes (0, 1] values always around the centre of the box, i.e. for this case in subscripts of -25 ~ +25, and shifts of +75 are specified in the MRC header to show its relative position with respect to the density map. Such masks must be converted so that they conform to the definition here for local symmetry imposition.
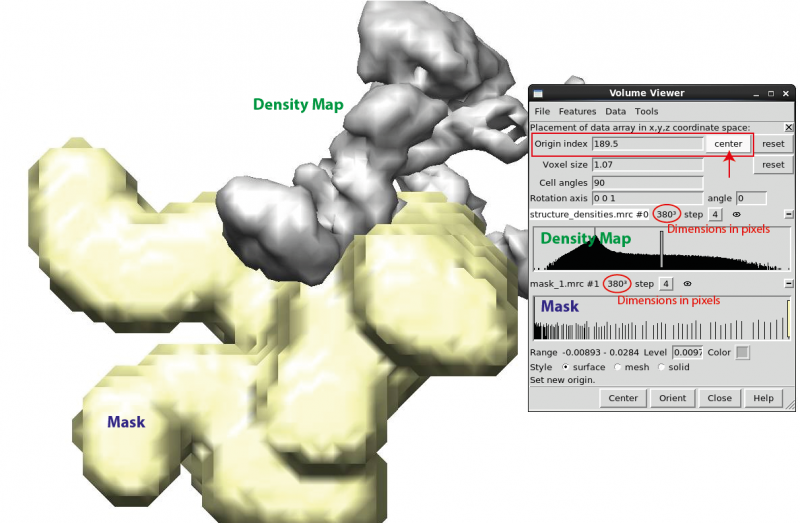
UCSF Chimera may be used to check a mask against the density map. Open both the 3D density map and the mask to be checked simultaneously ('chimera map.mrc mask.mrc'). First, check whether the map and the mask are of the same dimensions in pixels using the 'volume viewer' panel. Then find and click 'Coordinates' option under 'Features' menu on the same panel. Select and click 'center' for both the map and the mask. The 'origin index' values should now be the same for both files, and the mask should cover the designated subunit in the density map if the mask conforms to the local symmetry definition in RELION. If not, resample the mask on top of the density map (UCSF Chimera internal command ‘vop resample #2 onGrid #1’, if #1 and #2 denote the density map and mask files respectively) and save the resampled mask (#3, 'File -> Save map as' on the volume viewer panel). In a word, both the subunit densities and the mask values should be written to their absolute positions in the 3D data arrays in order to analyse the local symmetry.
Given a density map and all the required masks, all the operators are written into a single STAR format file, with each entry consists of a mask file name and a 6-parameter operator. Examples of local symmetry description STAR files can be found in the next two sections.
Local symmetry operators for microtubules with seams
You can skip this section and proceed onto the next if the target structure is not a microtubule with seam. This section introduces how to generate the mask and local symmetry operators for a 3-start 13-microtubule shown on the right in the schematic plot below. The mask and operators for microtubules with arbitrary numbers of proto-filaments can be generated accordingly.
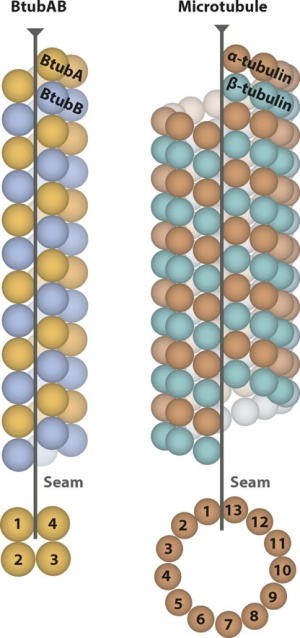
Assume that as seen in the top-view/bottom-view, the proto-filaments are numbered as #1~#13 clockwise/counter-clockwise. The proto-filaments closest to the seam are #1 and #13 while the one opposite to the seam is numbered as #7. If the number of proto-filaments is even, the mask should still cover one which is the farthest from the seam (e.g. either #2 or #3 for a 4-microtubule, either #6 or #7 for a 12-microtubule). Special requirements of the mask will be introduced in the next paragraph, here we focus on the calculation of the operators first. The helical symmetry is defined along each proto-filament: twist = +0.1 degrees, rise = 83.1 Angstroms in our 3-start 13-microtubule (with each pair of ab-tubulins treated as a subunit, or the building block of each proto-filament). In the local symmetry STAR file, the rot (or psi) angles are set to N*360/13 = N*27.69 degrees and the z translations are set to N*83.1*1.5/13 = N*9.59 Angstroms (N=-6~+6, without 0). All the other angles and translations are set to 0. Each of the 12 operators shows how to move the whole proto-filament #7 onto one of the other 12 by a rotation around the helical axis and a translation along the axis. The operators below have rot angles all set to 0. Since the tilts are all 0, it doesn't matter whether the rotation angles are given as rot or psi as they are equivalent.
data_ loop_ _rlnMaskName #1 _rlnAngleRot #2 _rlnAngleTilt #3 _rlnAnglePsi #4 _rlnOriginXAngst #5 _rlnOriginYAngst #6 _rlnOriginZAngst #7 mask-7.mrc 0.00 0.00 -27.692310 0.00 0.00 -9.59242 // Corresponds to the proto-filament #6 mask-7.mrc 0.00 0.00 -55.384621 0.00 0.00 -19.18484 // #5 mask-7.mrc 0.00 0.00 -83.076920 0.00 0.00 -28.77726 // #4 mask-7.mrc 0.00 0.00 -110.769234 0.00 0.00 -38.36968 // #3 mask-7.mrc 0.00 0.00 -138.461533 0.00 0.00 -47.96210 // #2 mask-7.mrc 0.00 0.00 -166.153854 0.00 0.00 -57.55452 // #1 mask-7.mrc 0.00 0.00 27.692310 0.00 0.00 9.59242 // #8 mask-7.mrc 0.00 0.00 55.384621 0.00 0.00 19.18484 // #9 mask-7.mrc 0.00 0.00 83.076920 0.00 0.00 28.77726 // #10 mask-7.mrc 0.00 0.00 110.769234 0.00 0.00 38.36968 // #11 mask-7.mrc 0.00 0.00 138.461533 0.00 0.00 47.96210 // #12 mask-7.mrc 0.00 0.00 166.153854 0.00 0.00 57.55452 // #13
In RELION 3.1, the columns rlnOriginX, rlnOriginY and rlnOriginZ are renamed to rlnOriginXAngst, rlnOriginYAngst and rlnOriginZAngst. Since the values were in Angstrom from the beginning, please update only the column names, not values.
The only mask covers the proto-filament #7, but only the central few tubulins along it. Because if the mask is made longer, some of the operators might translate the proto-filament too much along the z axis and move them out of the 3D particle box, causing improperly averaged densities. For example, if the particle box is 300 pixels (1.07 Angstroms per pixel) and the maximum absolute value of z translations in all the operators is 57.6 Angstroms, the mask along the proto-filament #7 should only cover the tubulins in the central 300*1.07-57.6*2=205.8 Angstroms, which is approximately ~64.1% of the box dimension. The mask must only covers the whole tubulins, without any incomplete parts.
As of 2020 November, the following sample files are temporarily unavailable.
Local symmetry STAR file (12 operators): ftp://ftp.mrc-lmb.cam.ac.uk/pub/she/localsym/localsym-3s13m.star
The only mask (binary, soft-edged, pixel size = 1.38 Angtroms): ftp://ftp.mrc-lmb.cam.ac.uk/pub/she/localsym/mask-7.mrc
The referential density map (pixel size = 1.38 Angstroms): ftp://ftp.mrc-lmb.cam.ac.uk/pub/she/localsym/ref-fil30.mrc
Although the map here has been low-pass filtered to 30 Angstroms (unpublished results from another group), it is recommended to use the best map you have to set up the local symmetry. Always display the referential map and the mask(s) simultaneously in UCSF Chimera for a check after you have constructed the mask(s).
It doesn't matter if you don't have a microtubule with seam as the starting reference. Given a referential 3-start 13-microtubule WITHOUT seam, you can just treat any proto-filament as #7 and the above mask and operators remain the same. The seam should become discernible after 3D auto-refinement if the local symmetry settings are correct.
[Remove this paragraph.] Enable the local symmetry option for such structure: Copy the referential density map, the mask and the local symmetry STAR file to the project directory. Add '--local_symmetry localsym-3s13m.star --tau2_fudge 13' as the additional option in 3D auto-refinement. We are still testing how '--tau2_fudge' influences the 3D reconstructions with local symmetry. Unreasonably large values lead to over-fitting but the subsequent post-processing step will always give you a fair resolution estimate.
Once helical 3D reconstructions lead to better density maps, the mask around the proto-filament might need to be re-generated. The rot (or psi) angles and the x, y, z translations might need to be improved as well. The local searches of symmetry operators are introduced in the section [XXXX].
Searching for arbitrary local symmetry operators
You can skip this section and proceed onto the next if the target structure is a microtubule with seam described in the previous section AND you are satisfied with the estimated operators. Refer to the last command in the section [XXX] if you want to improve the symmetry operators for a microtubule with seam.
List of masks
This section introduces a general approach of finding local symmetry operators for single-particle reconstructions. It requires the density map and the masks of all regions of interest as input (all in MRC format). An example structure consisting of a trimer bound to a tetramer (N=2, K1=3, K2=4) is used as an example. A total of 3+4=7 masks are required to mark all the regions of interest for calculating the operators, although only 2 masks (Mtri, Mtetra) are necessary in applying the symmetry after the operators are determined.
The density map and the masks converted from PDB models might lead to more accurate and stable operators. The same PDB model should be fitted to every set of identical regions and converted into MRC density maps of those local regions. Given an MRC density map, the standalone program ‘relion_mask_create’ writes out a soft-edged, binary mask:
relion_mask_create –-i Trimer_pdb1.mrc -–ini_threshold 0.01 –-extend_inimask 0 -–width_soft_edge 3 –-o Trimer_mask1.mrc
However, if the PDB structures are not readily available, a reconstruction result (e.g. from 3D reconstructions or post-processing) can be used as the input density map from which the masks are also generated.
Each mask must superimpose with the local region on the original density map when the mask and the map are centred at the same coordinates. The end of section 1 introduces such checks using UCSF Chimera. Once all the masks are ready, a STAR file ‘init_masklist.star’ with all the mask filenames should be generated manually, with the ith set of related regions marked using positive integer IDs. The STAR file below specifies ‘Trimer_mask1/2/3.mrc’ as the masks for all monomers in the trimer (ID = 1), and ‘Tetramer_mask1/2/3/4.mrc’ as the masks for all monomers in the tetramer (ID = 2).
data_ loop_ _rlnMaskName #1 _rlnAreaId #2 Trimer_mask1.mrc 1 Trimer_mask2.mrc 1 Trimer_mask3.mrc 1 Tetramer_mask1.mrc 2 Tetramer_mask2.mrc 2 Tetramer_mask3.mrc 2 Tetramer_mask4.mrc 2
Global searches of operators
The next step is to perform initial global searches of the corresponding local symmetry operators, given the original density map and the list of masks.
mpirun -n 40 relion_localsym_mpi --search --i_map partall_sums.mrc --i_op_mask_info init_masklist.star --o_mask_info maskinfo_iter000.star --angpix 1.34 --ang_step 5
The above command performs global orientation searches on three Euler angles ϕ, θ, ψ at an angular sampling rate of 5° using the density map ‘partall_sums.mrc’ (with a pixel size of 1.34Å) and the masks specified by ‘init_masklist.star’. MPI parallelisation distributes the workload equally onto 40 CPU cores for acceleration. A non-parallel version is also implemented as ‘relion_localsym --search’. For global searches, an angular step coarser than 5° might result in worse results with poorer convergence behaviour in the following local searching steps, and a much finer sampling may take too much computation time. For bigger maps (>= 300 pixels), binning the cropped boxes by a factor of 2 (additional option ‘--bin 2’) leads to better efficiency. The results are written into the local symmetry description file in STAR format (the Euler angles, _rlnAngle*, are in degrees and the translations, _rlnOrigin?, are in Angstroms).
data_ loop_ _rlnMaskName #1 _rlnAngleRot #2 _rlnAngleTilt #3 _rlnAnglePsi #4 _rlnOriginX #5 _rlnOriginY #6 _rlnOriginZ #7 Trimer_mask1.mrc -70.00 45.00 70.00 29.71 -7.65 -84.00 Trimer_mask1.mrc 155.00 30.00 175.00 -48.97 -32.08 121.36 Tetramer_mask1.mrc 130.00 70.00 -50.00 177.25 43.81 -131.91 Tetramer_mask1.mrc -70.00 55.00 55.00 17.07 -9.14 -89.64 Tetramer_mask1.mrc 110.00 30.00 -110.00 -33.46 -61.76 139.06
This is the exact format of a local symmetry description file for the purpose of imposing such symmetry in 3D reconstructions in RELION. Note that only one mask is used for each set of regions (‘Trimer_mask1.mrc’ for the trimer and ‘Tetramer_mask1.mrc’ for the tetramer) in this output STAR file and the number of operators for trimer and tetramer are K1-1=2 and K2-1=3. The centre-of-mass positions of other masks (*_mask2/3/4.mrc) can be deduced by the 2+3=5 operators, and thereby not explicitly kept in this STAR file.
Local searches of operators
The initially estimated operators need to be improved step-by-step. The same original density map must be used throughout the whole process of finding the operators and the filenames and densities of masks must also remain unchanged as well. Both the input density map and the translational operators in the local symmetry STAR file should also agree with the same pixel size. The command below locally refines the list of in operators ‘maskinfo_iter000.star’ and writes out ‘maskinfo_iter001.star’, using angular and translations searches of every 0.5° within ±2° and every 0.5Å within ±2Å respectively. The options '--offset_range 2 --offset_step 0.5' can be removed if only the angles are to be searched. Searching angles with translations fixed can be performed similarly by removing the 2 angle-related options.
mpirun -n 40 relion_localsym_mpi --search --i_map partall_sums.mrc --i_mask_info maskinfo_iter000.star --o_mask_info maskinfo_iter001.star --angpix 1.34 --ang_range 2 --ang_step 0.5 --offset_range 2 --offset_step 0.5 (--bin 2)
It is recommended to search either angles or translations in a single run to reduce computation time. The sampling rates are to be progressively decreased once the refined operators under the current rate remain stable. For better convergence, if the rate is to be decreased in the next run, the corresponding searching range is suggested to be >=2X the sampling rate of the current run. The translational searches (of the center-of-mass coordinates) are not expected to require large searching ranges (‘--offset_range X’, X is in Angstroms and usually an equivalence of ≤ 3X pixel size) as long as the input masks and densities are similar in every set of identical regions. The input STAR files can always be split into subsets of operators if any set of regions need different searching strategies from others, and combined before the actual 3D reconstructions. There is no need to search with very fine samplings (<0.1° or <0.1 pixels) as real-space interpolation errors become the dominant factor influencing the refined results. The optimal searching schemes may vary for different structures. For some structures, it might be worthwhile using the same settings several times until the refined values are all stabilised. Proceed the searches for all operators until all of them converge to required precisions (usually ~0.1° and ~0.1 pixels). Note that operators with low tilts (<+10°) are often not stable since the ϕ (_rlnAngleRot) and ψ (_rlnAnglePsi) angles are inseparable at very low θ (≤30°, _rlnAngleTilt) values. For such cases, the searching ranges of θ and either ϕ or ψ can be set to zero to limit the orientation refinements to only one Euler angle for stability. [restructure this piece of text???]
A general searching scheme below is designed for a pseudo-dimer test case (1 mask + 1 operator) so that each round lasts for ~2 minutes with ~100,000 samplings for the operator using a cropped box size of <100 pixels on a 30-core CPU machine (Intel Xeon E5-2643, 3.4~3.5 GHz). Optimal searching schemes vary across structures and available computing resources.
Round Angular Angular Translational Translational
Ranges p/m(°) Samplings (°) Ranges p/m(pix) Samplings (pix)
(Global) (All) 5 -- --
1 10 1 -- --
2 2 0.5 2 0.5
3 2 0.1 -- --
4 0.5 0.1 0.5 0.1
The following command gives an example of specifying various searching ranges for different angles/translations of the symmetry operators. Note that the ranges can be set to 0 if some of the angles/translations need not to be improved in a certain round (e.g. tilt=0 degrees for some microtubules with seams).
[put the command here - search for microtubules]
Verification of operators
One way to verify the optimised operators is to apply the local symmetry to a previously reconstructed density map (‘unsym.mrc’) and inspect the symmetrised densities (‘sym.mrc’) manually. The symmetrised regions on the output map should be at least as clear as the unsymmetrised regions on the input map if the correct local symmetry operators and masks (‘mask_and_operators.star’, similar to ‘maskinfo_iter000.star’ in the above section 4.2.5) are provided.
relion_localsym --apply --angpix 1.34 --i_map unsym.mrc --i_mask_info mask_and_operators.star --o_map sym.mrc
Verification can also be performed by replicating the masks according to the symmetry operators. This method might be beneficial for flexible complexes where some regions appear more blurry than their counterparts and applying local symmetry to the original map makes all regions vague:
relion_localsym --duplicate (--i_map unsym.mrc) --angpix 1.34 --i_mask_info mask_and_operators.star --o_map replicated.mrc
Imposing local symmetry in 3D reconstructions
Once the correct operators have been obtained, local symmetry can be applied in 3D classification/refinement jobs with the option ‘--local_symmetry mask_and_operators.star’. The initial reference should be set to the density map which has been used to generate the above operators. Imposition of local symmetry has masking effects in real-space so it is always disabled in the final iterations of 3D auto-refinement jobs where unfiltered half-maps are compared for Fourier-shell correlations. Unlike helical symmetry, local auto-refinement of local symmetry operators is not implemented during 3D reconstructions since there are 6 free parameters in every operator and the operators might diverge given a heavily low-pass filtered density map as the 3D initial reference. Therefore, the operators might need to be locally refined when better quality maps are reconstructed. In addition, the local symmetry given the same sets of operators can also be applied to a post-processed map [don’t put commands here, do them above].
The regularisation T value might need to be manually adjusted to account for the presence of local symmetry in a 3D reconstruction. T is 1 by default in 3D auto-refinements. However, for a 13-microtubule with seam introduced in section X, all the 13 proto-filaments contain the same information and it is expected that the local symmetry enhance the signals by 13 folds. Therefore, T=13 might seem more appropriate. For the similar reason, T=2 may be suitable for the pseudo-dimer in section X. However, the T value might be hard to choose when the structure includes multiple sets of identical regions or asymmetrical parts. A larger T can still be used in such cases, and the artefacts caused by over-fitting given a user-defined T can be removed after post-processing. Therefore, post-processing is always recommended if a T value other than one is used in 3D auto-refinements. The T value can be set as an additional argument ‘--tau2_fudge X’ in 3D auto-refinements. In addition, the regularisation parameter T can be found in ??? tab in the GUI and is T=4 by default for 3D classifications, where there are no gold-standard FSC correlations performed between data half-sets.
References
Thanks Sam Lacey and Shabih Shakeel from MRC Laboratory of Molecular Biology for their discussions.
[1] Deng, X., et al. (2017). Four-stranded mini microtubules formed by Prosthecobacter BtubAB show dynamic instability. Proceedings of the National Academy of Sciences, 114(29), E5950-E5958. PNAS
[2] Pettersen, Eric F., et al. "UCSF Chimera-a visualization system for exploratory research and analysis." Journal of computational chemistry 25.13 (2004): 1605-1612. PubMed